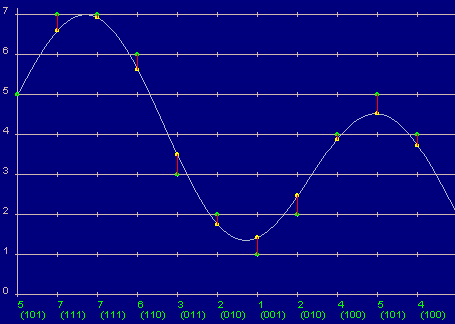
3. Kwantiseren

Na het sampelen hebben de signaalmonsters nog een analoge signaalwaarde die in principe iedere waarde binnen een bepaald bereik kan aannemen. Deze signaalwaarden worden vervolgens gekwantiseerd. Dit houdt in dat de signaalwaarde wordt afgerond tot een digitaal getal dat -meestal binair- wordt gecodeerd. Dit proces wordt ook wel PulsCodeModulatie genoemd. Hierbij wordt altijd een afrondingsfout gemaakt. De AD-conversie van een analoog signaal in een binaire bitstroom is geïllustreerd in onderstaande figuur. Van het analoge signaal wordt op gezette tijden de waarde bepaald (de gele punten). Deze momentane waarden worden vervolgens afgerond (de groene punten) en omgezet in een digitale waarde (de groene waarde onderin).

AD-conversie. (Klik op het plaatje voor een demo-applet)

Het aantal bits dat hierbij wordt gebruikt, is bepalend voor de afrondingsfout (rood). Deze afrondingfout wordt ook wel de kwantiseringsfout of kwantiseringsruis genoemd.

Deze fout kan worden gezien als een foutsignaal dat aan het oorspronkelijke signaal wordt toegevoegd en geeft na de DA-conversie een ruisachtig effect. We spreken in dit verband dan ook van kwantiseringsruis. Deze extra ruis is niet meer uit het signaal te verwijderen. Een ruisvrij signaal dat wordt gedigitaliseerd zal dus na digitalisatie altijd een beperkt signaal-ruisverhouding hebben. In dit verband wordt dan ook wel gesproken van een signaal-kwantiseringsruisverhouding (verder SQR). De kwantiseringsfout wordt kleiner naarmate het aantal bits per codewoord toeneemt. De SQR neemt dus toe als het aantal bits per codewoord toeneemt. Maar hoeveel neemt deze dan toe?

Dit is het eenvoudigst te illustreren met een voorbeeld: Stel we hebben een ruisvrij ingangssignaal dat ligt tussen de -1 V en +1 Volt. Als dit signaal met 4 bits wordt gecodeerd, wordt het bereik van 2 V verdeeld in 16 niveaus met een stapgrootte tussen de niveau's van 125 mV. Ingangswaarden die een halve stapgrootte boven of onder een niveau liggen worden bij de kwantisatie afgerond tot het betreffende niveau. De afrondingsfout die dan wordt gemaakt ligt tussen de -62,5 mV en + 62,5 mV. Als er met 5 bits wordt gecodeerd, dan wordt het aantal niveau's verdubbeld en de stapgrootte gehalveerd. De afrondingsfout wordt nu dus ook gehalveerd tot maximaal ±31,25 mV. Hieruit kunnen we dus de conclusie trekken dat de SQR een factor 2 of 6 dB toeneemt per extra bit.

De SQR is dan ook gelijk aan:

SQR = 6·n + (correctiefactor) dB.

De correctiefactor is afhankelijk van het ingangssignaal. De grootte van de SQR is namelijk afhankelijk van de momentane signaalwaarde van het ingangssignaal. De SQR is dan ook maximaal bij een maximaal ingangssignaalniveau en wordt ongunstiger bij afnemend signaalniveau.

We lichten dit toe met een voorbeeld: Neem een AD-convertor met een ingangssignaal dat kan variëren tussen 0 en 63 V. Stel er wordt gekwantiseerd met 6 bits. Hierdoor zijn er 64 kwantiseringsniveau's (0, 1, 2, .. 63 V) met een stapgrootte van 1 Volt. Een zwak signaal dat een signaalwaarde heeft van 0,5 V zal dan worden afgerond tot een signaal van 1 V. De signaal-kwantiseringsruisverhouding bedraagt dan 0.5/0,5 is 1. Een sterk signaal met een signaalwaarde van 62,5 V zal worden afgerond tot 63 V. De signaal-kwantiserings-ruisverhouding bedraagt voor dit signaal 62,5/0,5 = 125.

Voor een sinusvormig ingangssignaal met een maximale amplitude is de correctiefactor gelijk aan 1,76 dB. Bij de specificaties van een CD-speler (16 bit ) wordt dan ook vaak een signaal-ruisverhouding tussen de 96 dB en 98 dB aangegeven. Voor unipolaire signalen zoals video is de correctiefactor bij maximale uitsturing gelijk aan 10,8 dB. In de praktijk zal het signaal zich gemiddeld ruim onder de maximale uitsturing bevinden. De correctiefactor is dan ook eerder negatief dan positief.

In de praktijk is het ingangssignaal nooit geheel ruisvrij. Het aantal bits moet nu zodanig worden gekozen dat de ruistoename ten gevolge van de kwantisering verwaarloosbaar is ten opzichte van de in het signaal aanwezige ruisniveau. Het aantal bits wordt niet groter gekozen dan noodzakelijk omdat dan de hoeveelheid bits per tijdseenheid en daarmee de voor transport benodigde bandbreedte toeneemt. Om een voorbeeld te geven: voor een analoog telefoonsignaal is een signaal-ruisverhouding van 36 dB heel gewoon. Het heeft dus geen zin om een telefoonsignaal met dezelfde precisie als audio te gaan beschrijven, omdat dan de op de lijn aanwezige ruis wordt vastgelegd.

Bij signalen die slechts zeer langzaam veranderen en dus lang op min of meer dezelfde waarde blijven hangen, wordt wel gebruik gemaakt van dithering. Aan het signaal wordt een kleine hoeveelheid ruis toegevoegd. Het effect hiervan kan het best met behulp van een voorbeeld worden verduidelijkt. Stel dat een analoog ingangssignaal varieert tussen 0 en 4,095 V en met 12-bit wordt gedigitaliseerd, waardoor het digitale signaal de waarden 0 tot en met 4095 kan aannemen. Stel nu dat het analoge ingangssignaal lang (neem voor het gemak zo'n 10.000 samples) op 3,0001 V blijft hangen. Het signaal wordt nu constant op het digitale niveau 3000 afgerond. Door er een kleine hoeveelheid ruis aan te voegen, zal het signaal af en toe (in het ideale geval voor 10%) worden afgerond op 3001, waardoor het gemiddelde signaalniveau op 3000.1 uitkomt als er 10.000 samples worden genomen.